


| Carlos Campos Álvarez |
|
Teaching Units | Home |
| 2.2 Velocity in the S.H.M. |
|
The velocity of
a moving body which describes an S.H.M. is obtained from the derivative
of the position with respect to
time:
If we again keep to the simplest case, in which the phase difference φ= 0 , the equation is simplified:
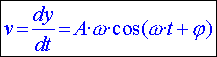  |