As mentioned, the position of a body which describes an S.H.M. is given by a sinusoidal type equation:         

The simplest case occurs when there is no phase difference (φ=0). In this case the equation is reduced to:          

Click on next to see the graph of this function.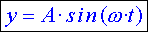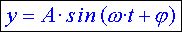